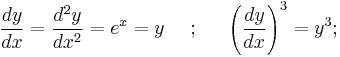Inverse functions and differentiation
In mathematics, the inverse of a function 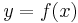 is a function that, in some fashion, "undoes" the effect of
is a function that, in some fashion, "undoes" the effect of  (see inverse function for a formal and detailed definition). The inverse of
(see inverse function for a formal and detailed definition). The inverse of  is denoted
is denoted 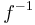 . The statements y = f(x) and x = f −1(y) are equivalent.
. The statements y = f(x) and x = f −1(y) are equivalent.
Their two derivatives, assuming they exist, are reciprocal, as the Leibniz notation suggests; that is:
This is a direct consequence of the chain rule, since
and the derivative of  with respect to
with respect to  is 1.
is 1.
Writing explicitly the dependence of  on
on  and the point at which the differentiation takes place and using Lagrange's notation, the formula for the derivative of the inverse becomes
and the point at which the differentiation takes place and using Lagrange's notation, the formula for the derivative of the inverse becomes
Geometrically, a function and inverse function have graphs that are reflections, in the line y = x. This reflection operation turns the gradient of any line into its reciprocal.
Assuming that  has an inverse in a neighbourhood of
has an inverse in a neighbourhood of  and that its derivative at that point is non-zero, its inverse is guaranteed to be differentiable at
and that its derivative at that point is non-zero, its inverse is guaranteed to be differentiable at  and have a derivative given by the above formula.
and have a derivative given by the above formula.
Contents |
Examples
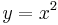 (for positive
(for positive  ) has inverse
) has inverse 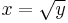 .
.
At x = 0, however, there is a problem: the graph of the square root function becomes vertical, corresponding to a horizontal tangent for the square function.
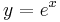 has inverse
has inverse 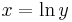 (for positive
(for positive  )
)
Additional properties
- Integrating this relationship gives
- This is only useful if the integral exists. In particular we need
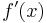 to be non-zero across the range of integration.
to be non-zero across the range of integration.
- It follows that functions with continuous derivative have inverses in a neighbourhood of every point where the derivative is non-zero. This need not be true if the derivative is not continuous.
Higher derivatives
The chain rule given above is obtained by differentiating the identity x = f −1(f(x)) with respect to x. One can continue the same process for higher derivatives. Differentiating the identity with respect to x two times, one obtains
or replacing the first derivative using the formula above,
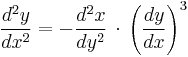 .
.
Similarly for the third derivative:
or using the formula for the second derivative,
These formulas are generalized by the Faà di Bruno's formula.
These formulas can also be written using Lagrange's notation. If f and g are inverses, then
Example
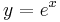 has the inverse
has the inverse 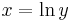 . Using the formula for the second derivative of the inverse function,
. Using the formula for the second derivative of the inverse function,
so that
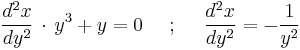 ,
,
which agrees with the direct calculation.
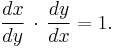
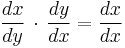
![\left[f^{-1}\right]'(a)=\frac{1}{f'\left( f^{-1}(a) \right)}](/2012-wikipedia_en_all_nopic_01_2012/I/26df0c77ef6202cc3c87f07421576150.png)
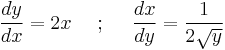
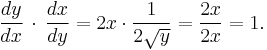
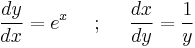
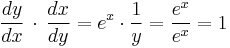
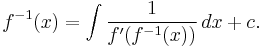
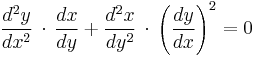
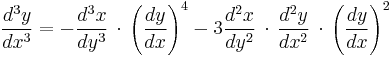
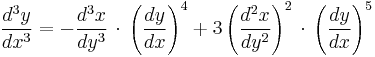
![g''(x) = \frac{-f''(g(x))}{[f'(g(x))]^3}](/2012-wikipedia_en_all_nopic_01_2012/I/8f100ebd506b106996881feaf6e333e1.png)